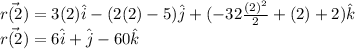Answer:
The velocity vector is
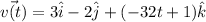 and the position vector is
and the position vector is
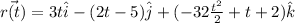
When t = 2 the position is
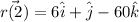
Explanation:
To find the position function, you should integrate twice, each time using one of the initial conditions to solve for the constant of integration. The velocity vector is
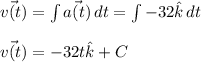
where
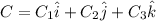 .
.
Letting t = 0 and applying the initial condition
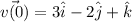
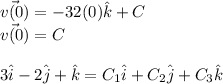
Therefore,
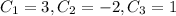
So, the velocity at any time t is
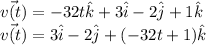
Integrating once more produces
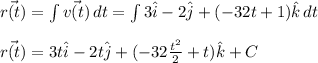
Letting t = 0 and applying the initial condition
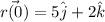
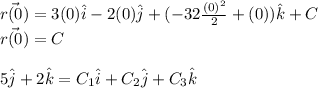
Therefore,
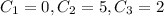
The position vector is
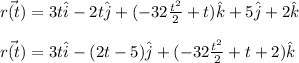
When t = 2 the position is