Answer:
a) 2
b) 3
c) 1
Explanation:
The standard error (SE) is given as:
SE = s ÷ √n
here,
s = √[SS ÷ (n - 1)]
Therefore,
We get,
SE =
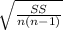
Therefore,
For a) n = 4 with SS = 48
SE =
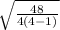
or
SE = √4
or
SE = 2
For b) n = 6 with SS = 270
SE =
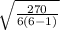
or
SE = √9
or
SE = 3
For c) n = 12 with SS = 132
SE =
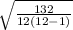
or
SE = √1
or
SE = 1