Question

n is a positive integer with exactly two different divisors greater than 1, how many positive factors does n^2 have? A. 4 B. 5 C. 6 D. 8 E. 9

Answer 1

A positive integer n with only two divisors greater than 1 is a prime number. When squared, n2 has exactly 4 positive factors: 1, n, n², and n itself.

Step-by-step explanation:

If n is a positive integer with exactly two different divisors greater than 1, then n must be prime. Hence, the prime number n only has 1 and itself as its divisors. When we square n, that is n2, the total number of divisors becomes the following:

• 1
• n
• n2
• n itself since a prime squared still has the prime as a factor

The total count of the positive factors of n2 is thus 4, which includes 1, n, n2, and n. Therefore, the correct answer is A. 4.

Answer 2

C. 5

Step-by-step explanation:

Remember that for any integer
`n`, the integers
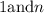`1 \text{and} n` are both divisors (or factors) of
`n`. First, we will prove that n is a square, and then we will compute the factors of the n².

In this case, the integer n has exactly two different divisors greater than 1. It's impossible that
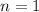`n=1`, since 1 doesn't have positive factors greater than 1. Then
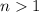`n>1`, therefore
`n` itself is one of the required divisors. Denote by
`a` the other divisor greater than 1, and note that to satisfy the condition on the divisors,
`a<n`.

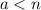Because a divides n, there exists some integer
`k` such that
`n=ak`. We must have that
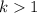`k>1`, if not, then
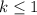`k\leq 1`, which implies that
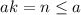`ak=n\leq a`, which contradicts the part above.

Now,
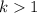`k>1` and, by definition of divisibility, k divides n. Then k must be equal either to n or a, since we can't have three different divisors of this kind. If
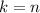`k=n` then
`n=an` and by cancellation,
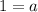`1=a` which is a contradiction. Therefore
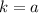`k=a` and
`n=a^2`.

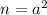We have that
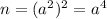`n=(a^2)^2=a^4`. We can write n as
`n=a^3a=a^2a^2=a^4 \cdot 1`. From the first equation, a divides n and a³ divides n. From the second equation, a² divides, and from the last one, 1 divides n and a⁴=n divides n. Thus n has exactly 5 positive factors.