Question

A circular rod with a gage length of 3.5 mm and a diameter of 2.8 cmcm is subjected to an axial load of 68 kN . If the modulus of elasticity is 200 GPa, what is the change in length?

Answer 1

To solve this problem, we will apply the concepts related to the linear deformation of a body given by the relationship between the load applied over a given length, acting by the corresponding area unit and the modulus of elasticity. The mathematical representation of this is given as:

`\delta = (PL)/(AE)`

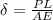
Where,

P = Axial Load

l = Gage length

A = Cross-sectional Area

E = Modulus of Elasticity

Our values are given as,

l = 3.5m

D = 0.028m

`P = 68*10^3 N`

E = 200GPa

`A = (\pi)/(4)(0.028)^2 \rightarrow 0.0006157m^2`

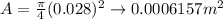
Replacing we have,

`\delta = (PL)/(AE)`

`\delta = (( 68*10^3)(3.5))/((0.0006157)(200*10^9))`

`\delta = 0.001932m`

`\delta = 1.93mm`

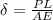
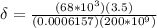
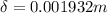
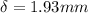
Therefore the change in length is 1.93mm