To solve this problem we will use the work theorem which describes the change of force in proportion to the distance traveled.
Our function is given as:
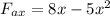
PART A) The maximum work is given in the position in which the function of the Force is equal to zero, therefore
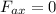
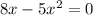
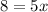
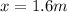
PART B) The maximum work done is given from the 0 position to the maximum work distance, therefore:
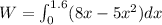
![W = \Big[(8x^2)/(2)-(5x^3)/(3)\Big]^(1.6)_0](https://img.qammunity.org/2020/formulas/physics/college/sozalz7khjk75gfw9dpk54or3sqybz2haq.png)
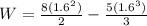
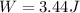
PART C) At the moment when the work reaches zero, we will simply match the integral previously found to zero value so
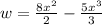
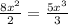
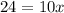
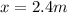
PART D ) If the work is zero in position 2.4, do not open movement, as the distance to travel will also be 0. The body will be at rest again 2.4m from its initial position.