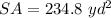Question

10 POINTS

Find the surface area of the regular pyramid. Round to the nearest tenth if necessary.

Answer 1

234.8 is correct.

Explanation:

Answer 2

`SA=234.8\ yd^2`

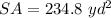
Explanation:

we know that

The surface area of the regular pyramid is equal to the area of the triangular base plus the area of its three triangular lateral faces

step 1

Find the area of the triangular base

we know that

The triangular base is an equilateral triangle

so

The area applying the law of sines is equal to

`A=(1)/(2)(14^2)sin(60^o)`

`A=(1)/(2)(196)(√(3))/(2)`

`A=49√(3)=84.87\ yd^2`

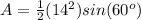
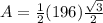
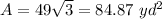
step 2

Find the area of its three triangular lateral faces

`A=3[(1)/(2)bh]`

we have

`b=14\ yd`

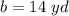
Find the height of triangles

Applying the Pythagorean Theorem

`10^2=(14/2)^2+h^2`

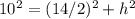
solve for h

`100=49+h^2`

`h^2=100-49`

`h=√(51)\ yd`

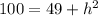
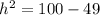
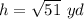
substitute

`A=3[(1)/(2)(14)√(51)]`

`A=149.97\ yd^2`

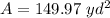
step 3

Find the surface area

Adds the areas

`SA=84.87+149.97=234.84\ yd^2`

Round to the nearest tenth

`SA=234.8\ yd^2`