Question

Each one of four people will request either Coke D Let X denote the number that request Coke, where the remainder request Sprite. The probability distribution of X is given above. (For instance the probability exactly 3 request coke is 0.33) X 0 | 1 | 2 | 3 | 4 or Sprite. PCX = x) 0.09 0.15 0.18 0.33 0.25 a) (Compute the mean "E(X)" and variance "V(X)": b) If Cokes cost $5 each and Sprites cost $3 each, then find E(R) and V(R) (mean and variance) where R is the revenue generated from the sale of the four drinks, assuming all get, and pay for, the drink they requested. (Hint: write R as a function of X) c) Suppose there are only 3 Cokes and 3 Sprites available. What is the probability that when the four make their orders, everyone gets what they ordered?

Answer 1

a) E(x)=2.5 V(x)=1.59

b) E(R)=17 V(R)=6.36

c) The probability that, when the four make their orders, everyone gets what they ordered is P=0.66.

Explanation:

a) The mean E(x) can be calculated as:

`E(x)=\sum^4_(i=0) p_ix_i\\\\E(x)=0.09*0+0.15*1+0.18*2+0.33*3+0.25*4\\\\E(x)=0.00+0.15+0.36+0.99+1.00\\\\E(x)=2.5`

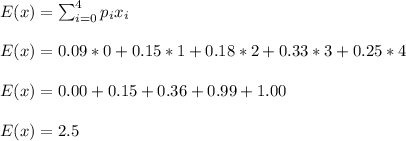
The variance V(x) can be calculated as:

`V(x)=\sum^4_(i=0) p_i(x_i-\bar x)^2\\\\V(x)=0.09(0-2.5)^2+0.15(1-2.5)^2+0.18(2-2.5)^2+0.33(3-2.5)^2+0.25(3-2.5)^2\\\\V(x)=0.09*6.25+0.15*2.25+0.18*0.25+0.33*0.25+0.25*2.25\\\\V(x)=0.5625+0.3375+0.045+0.0825+0.5625\\\\V(x)=1.59`

b) The revenue can be expressed as:

`R=5*x+3*(4-x)`

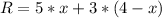
Then, the expected value of R canbe expressed in function of x:

`E(R)=E(5x+3(4-x))=5E(x)+3(4-E(x))\\\\E(R)=5*2.5+3(4-2.5)=12.5+4.5=17`

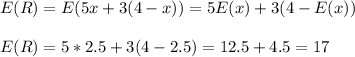
The expected revenue is $17.

The variance of R is

`V(R)=V(5*x+3(4-x))=V(5x+12-3x)=V(2x+12)\\\\V(R)=V(2x)+V(12)=2^2V(x)+0=4*1.59\\\\V(R)=6.36`

c) In the case there are only 3 Cokes and 3 Sprites available, the only orders that can not be fullfilled are when X=0 (they order 4 Sprites) and X=4 (they order 4 Cokes).

The probability of these events is:

`P(x=0,x=4)=P(x=0)+P(x=4)=0.09+0.25=0.34`

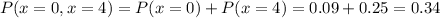
So, the probability of everyoned getting what they ordered is:

`P=1-P(x=0,x=4)=1-0.34=0.66`

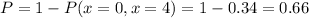
The probability that, when the four make their orders, everyone gets what they ordered is P=0.66.