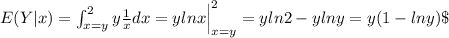Question

Let X have the uniform distribution U(0, 2) and let the conditional distribution of Y , given that X = x, be U(0, x). Find the joint p.d.f. f(x, y) of X and Y , and be sure to state the domain of f(x, y). Find E(Y |x)

Answer 1

`f(x,y) = (1)/(x) (1)/(2)= (1)/(2x) , 0\leq x \leq 2 , 0\leq y \leq x`

`E(Y|x) = \int_(x=y)^2 y (1)/(x) dx= y ln x \Big|_(x=y)^2 =y ln 2 -y ln y = y(1-lny) \`

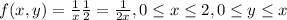
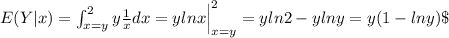
Explanation:

We have two random variables X and Y.
`X \sim Unif(0,2)` and given that X=x, Y has uniform distribution (0,x)

From the definition of the uniform distribution we have the densities for each random variable given by:

`f_X (x) =(1)/(2) , 0\leq x\leq 2`

`f_(Y|X) (y|x) = (1)/(x), 0\leq y \leq x`

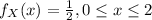
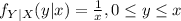
And on this case we can find the joint density with the following formula:

`f(x,y) = f_(Y|X)(y|x) f_X (x)`

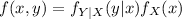
And multiplying the densities we got this:

`f(x,y) = (1)/(x) (1)/(2)= (1)/(2x) , 0\leq x \leq 2 , 0\leq y \leq x`

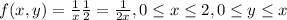
Now with the joint density we can find the expected value E(Y|x) with the following formula:

`E(Y|x) = \int y f_(Y|X)(y|x)dx`

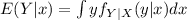
And replacing we got:

`E(Y|x) = \int_(x=y)^2 y (1)/(x) dx= y ln x \Big|_(x=y)^2 =y ln 2 -y ln y = y(1-lny) \`