Question

Is tangent to the circle with center at B. The measure of ∠ACB is 24°.What is the measure of ∠ABC? Enter your answer in the box.m∠ABC = °Circle B with a tangent, a chord, and a line segment. Point A is at 12 o clock on the circle. Point C is at 2 o clock outside of the circle. Chord A B and segment B C meet at point B in the center. Tangent A C passes through point C.

Answer 1

32

Explanation:

took the test and got it correct - k12

Answer 2

`m\angle ABC=180`

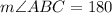
Explanation:

We are given that a circle with center B .

`m\angle ACB=24^(\circ)`

AC is a tangent to the circle B.

We have to find the measure of angle ABC.

We know that

Radius is perpendicular to tangent.

Therefore,
`m\angle BAC=90^(\circ)`

In triangle ABC

`m\angle ABC+m\angle ACB+m\angle BAC=180^(\circ)`

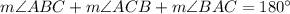
By using angles sum property of triangle

Substitute the values then we get

`24+90+m\angle ABC=180`

`114+m\angle ABC=180`

`m\angle ABC=180-114=66^(\circ)`

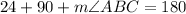
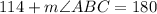
Hence, the measure of angle ABC=66 degrees