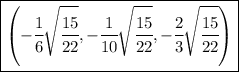Question

Find the points on the surface 3x2+5y2+3z2=13x2+5y2+3z2=1 at which the tangent plane is parallel to the plane 1x+1y+4z=71x+1y+4z=7.

Answer 1

The points are
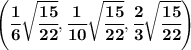`\bold{\left(  \cfrac{1}6\sqrt{\cfrac {15}{22}} ,\cfrac 1{10}\sqrt{\cfrac {15}{22}},\cfrac{2}3\sqrt{\cfrac {15}{22}}\right)}` and
`\bold{\left(  -\cfrac{1}6\sqrt{\cfrac {15}{22}} ,-\cfrac 1{10}\sqrt{\cfrac {15}{22}},-\cfrac{2}3\sqrt{\cfrac {15}{22}}\right)}`

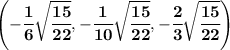
Explanation:

We can find the normal to both the surface and the plane, and set a relation between them since tangent plane and the given are parallel. Once we have that we can use the original surface to find the points on the surface that are tangent to the plane.

Normal vectors.

The normal vectors can be found using partial derivatives or gradient, thus we can call the surface:

`F(x,y,z)=3x^2+5y^2+3z^2-1=0`

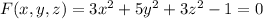
So its normal is

`\vec n_1 = \left< \cfrac{\partial F}{\partial x},\cfrac{\partial F}{\partial y},\cfrac{\partial F}{\partial z} \right>\\\vec n_1= \left< 6x,10y,6z\right>`

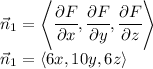
And the normal vector to the plane is

`\vec n_2= < 1,1,4>`

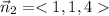
Notice that the normal vector of the plane is just represented by the coefficients of x,y and z.

Parallel condition

The two planes are parallel only if their normal vectors are parallel as well, so we can write

`\vec n_1=t\vec n_2`

Using the previously found normal vectors.

`\left< 6x,10y,6z\right>=t< 1,1,4>`

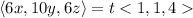
So we get

`x= t/6\\y=t/10\\z=2t/3`

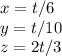
Finding the points where we have the tangent plane.

We can plug the expressions we have found of x, y and z on the given surface equation.

`3(t/6)^2+5(t/10)^2+3(2t/3)^2=1`

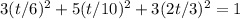
And we can simplify and solve for t.

`\cfrac{t^2}{12}+\cfrac{t^2}{20}+\cfrac{4t^2}{3}=1`

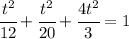
The LCD is 60 so we can multiply all terms in both sides by 60 to get

`5t^2+3t^2+80t^2=60\\88t^2=60`

So we get

`t^2  = \cfrac {15}{22}`

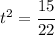
That give us the values of t

`t_(1,2) =\pm \sqrt{\cfrac {15}{22}}`

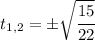
Lastly at
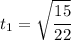`t_1=\sqrt{\cfrac {15}{22}}` we have:

`x= \cfrac{1}6\sqrt{\cfrac {15}{22}} \\y=\cfrac 1{10}\sqrt{\cfrac {15}{22}}\\z=\cfrac{2}3\sqrt{\cfrac {15}{22}}`

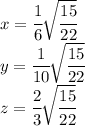
So one point is

`\boxed{\left(  \cfrac{1}6\sqrt{\cfrac {15}{22}} ,\cfrac 1{10}\sqrt{\cfrac {15}{22}},\cfrac{2}3\sqrt{\cfrac {15}{22}}\right)}`

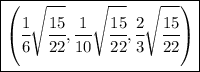
And for the value of
`t_2=-\sqrt{\cfrac {15}{22}}`

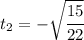
We have

`x= -\cfrac{1}6\sqrt{\cfrac {15}{22}} \\y=-\cfrac 1{10}\sqrt{\cfrac {15}{22}}\\z=-\cfrac{2}3\sqrt{\cfrac {15}{22}}`

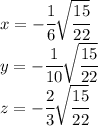
So the second point is

`\boxed{\left( - \cfrac{1}6\sqrt{\cfrac {15}{22}} ,-\cfrac 1{10}\sqrt{\cfrac {15}{22}},-\cfrac{2}3\sqrt{\cfrac {15}{22}}\right)}`