Question

A man stands at the center of a platform that rotates without friction with an angular speed of 3.95 rev/s. His arms are outstretched, and he holds a heavy weight in each hand. The moment of inertia of the man, the extended weights, and the platform is 12.5 kg*m^2. When the man pulls the weights inward toward his body, the moment of inertia decreases to 2.5 kg*m^2. What is the resulting angular speed of the platform?

Answer 1

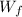`W_f`= 124.05 rad/s

Step-by-step explanation:

Using the conservation of the angular momentum:

`L_i = L_f`

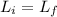
so:

`I_iW_i = I_fW_f`

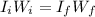
where
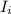`I_i` is the initial moment of inertia,
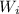`W_i` the initial angular velocity,
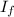`I_f` the final moment of inerta and
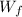`W_f` the final angular velocity.

Note: Wi = 3.95 rev/s = 24.81 rad/s

Then, replacing values, we get:

`(12.5)(24.81rad/s) = (2.5)W_f`

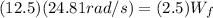
Finally, solving for
`W_f`:

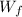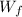`W_f`= 124.05 rad/s