Question

. The area of a rectangle is 64 square inches. Express the perimeter P as a function of the w

and state the domain.

Answer 1

Perimeter P=2x+ (128/x)

Step-by-step explanation

Area = L*W

Perimeter = 2L + 2W

one side is x meters

area = 64 sq.inches

the other side will be 64/x.

the perimeter P = 2L+2W

P= 2x+ (2*64/x)

P=2x+ (128/x)

Answer 2

Explanation:

The area of a rectangle is A = lw. If the area is 64, we sub it in to get 64 = lw.

If we want to express the perimeter in terms of w using that area expression, we solve the area for l:

`l=(64)/(w)`

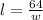
The formula for the perimeter of a rectangle is

P = 2l + 2w

If we are to express it in terms of w, sub in the l value from the area:

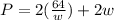`P=2((64)/(w))+2w` which simplifies to

`P=(128)/(w)+2w`

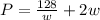
Because this is width and width is a distance measure, it can't ever be negative or 0, so the domain for w is w > 0.