Question

The pilot of an airplane flying at an elevation of 5000 feet sights two trees that are 300 feet apart. If the angle of depression to the base of the tree closer to him is 33˚, determine the angle of the depression to the second tree.

Answer 1

32°

Step-by-step explanation:

From the diagrammatic representation of the question,

Point A is the pilot point of view from the airplane

Point C is the foot of the first tree

Point D is the foot of the second tree

Line AB is the height of the airplane from the ground level.

Line CD is the distance between the two trees

Considering ΔABC,

tan 33°
`= (5000)/(BC)`

BC = 5000 / tan 33°

`BC = (5000)/(0.6494)`

BC = 7,699.41 feet

BD = BC + CD

BD = 7,699.41 + 300

BD = 7,999.41 feet

Considering ΔABD,

tan θ
`= (AB)/(BD)`

tan θ
`= (5000)/(7,999.41)`

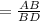
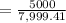
tan θ = 0.6250

θ = tan⁻¹ 0.6250

θ = 32°