Question

A mass weighing 30 lbstretches a spring . The mass is also attached to a damper with coefficient . Determine the value of for which the system is critically damped. Assume that .

Answer 1

the damping coefficient when the system is critically damped is 13.42 lb s/ft.

Step-by-step explanation:

The directions are missing the last part, which is:

"A mass weighing 30 lb stretches a spring 7.5 in. The mass is also attached to a damper with coefficient γ. Determine the value of γ for which the system is critically damped. Assume that
`g = 32 \cfrac {ft}{s^2}`

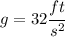
Round your answer to three decimal places."

The spring system is determined by the following differential equation

`my''+\gamma y'+ky=0`

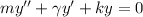
where
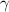`\gamma` is the damping coefficient, thus it is critically damped when the system transitions from real to complex solutions that happens at

`\gamma_^2 -4km=0`

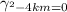
Solving for the damping coefficient.

`\gamma^2 = 4km\\ \gamma = √(4km)`

where the spring constant k is given by

`k = \cfrac{mg}{L}\\k = \cfrac wL\\`

And the mass is given by

`mg = w\\ m = \cfrac wg`

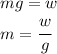
So the damping coefficient will be

`\gamma = √(4\cfrac wL \cfrac wg)\\\gamma = \sqrt{4\cfrac {w^2}{gL}}`

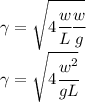
Replacing the given information we have:

`\gamma = \sqrt{4\cfrac {(30\, lbs)^2}{32\cfrac{ft}{s^2}0.625 ft}`

Thus we get

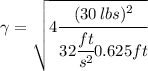
`\gamma = 13.42 \cfrac{lb \cdot s}{ft}`

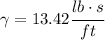
The value of the damping coefficient when the system is critically damped is 13.42 lb s/ft.