Question

On an asteroid, the density of dust particles at a height of 3 cm is ~30% of its value just above the surface of the asteroid. Assuming the temperature is 20 K and the average dust-particle mass is 10-19 kg. Estimate the gravitational acceleration on the asteroid.a. 2 m/s^2b. 10 m/s^2c. 0.1m/s^2

Answer 1

From the law of atmosphere

`N_v(y) = n_0*e^{-(mgy)/(Kb*T)}`

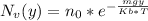
Where

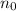`n_0` = constant and is number density where the height y = 0cm

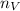`n_V` = Number density at height y=3cm

Kb = Boltzmann constant
`= 1.38*10^(-23)J/K`

`T=20K`

`m = 10^(-19)kg`

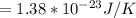
Re-arranging the equation to have the value of the gravity,

`(N_v(y))/(n_0) = e^{-(mghy)/(KbT)}`

`ln((N_v(y))/(n_0)) = -(mgy)/(KbT)`

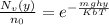
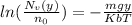
Since it is 30% of value above surface, therefore
`N_v = 0.3n_0`

`ln((0.3n_0)/(n_0)) = -(mgy)/(KbT)`

`g = -(KbT ln(0.3))/(my)`

`g = -((1.38*10^(-23)J/K)(20K)(Ln(0.3)))/(10^(-19)(3*10^(-2)))`

`g = (1.38*2*ln(0.3)*10^(-22))/(3*10^(-4))`

`g = 1.104*10^(-1)m/s^2`

`g = 0.1m/s^2`

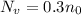
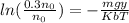
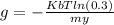
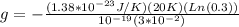
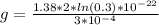
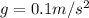
Therefore the correct answer is C.