Question

Photoelectrons are observed when a metal is illuminated by light with a wavelength less than 383 nm. What is the metal's work function?

Answer 1

5.19 x 10^-19 J

Step-by-step explanation:

threshold wavelength, λo = 383 nm = 383 x 10^-9 m

Work function,

`\phi =(hc)/(\lambda _(0))`

`\phi =(6.63*10^(-34)* 3 * 10^(8))/(383* 10^(-9))`

Ф = 5.19 x 10^-19 J

Answer 2

Work function of the metal is 3.24 eV.

Step-by-step explanation:

It is given that,

Wavelength,
`\lambda=383* 10^(-9)\ m`

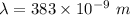
Let W is the work function of the metal. It is given by using Einstein's photoelectric effect equation. It is given by :

`W=(hc)/(\lambda)`

`W=(6.63* 10^(-34)* 3* 10^8)/(383* 10^(-9))`

`W=5.193* 10^(-19)\ J`

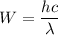
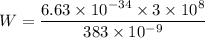
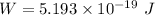
Since,
`1\ eV=1.6* 10^(-19)\ J`

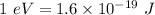
So, W = 3.24 eV

So, the work function of the metal is 3.24 eV. Hence, this is the required solution.