Question

On January 1, 2017, Bridgeport Corporation issued $620,000 of 9% bonds, due in 8 years. The bonds were issued for $586,402, and pay interest each July 1 and January 1. Bridgeport uses the effective-interest method.

Answer 1

cash 586,402 debit

discount on BP 33,598 debit

bonds payable 620,000 credit

--to record issuance of bonds--

interest expense 29320.1 debit

discount on BP 1420.1 credit

cash 27900 credit

--to record first interest payment--

Step-by-step explanation:

procceds 586,402

face value (620,000)

discount on bonds payable (33,598)

We need to solve for the effective market rate, which is done with excel or trial and error, we need to find which discount rate generates the coupon and maturity of the bond equal 586,402 dollars

As this is a discount we know it has to be higher than the bond rate.

We try and solve:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 620,000 x 9% / 2 = 27,900.00

time 16 ( 8 years x 2 payment per year)

rate 0.05

`27900 * (1-(1+0.05)^(-16) )/(0.05) = PV\\`

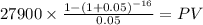
PV $302,373.7707

`(Maturity)/((1 + rate)^(time) ) = PV`

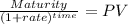
Maturity 620,000.00

time 16.00

rate 0.05

`(620000)/((1 + 0.05)^(16) ) = PV`

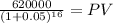
PV 284,029.14

PV c $302,373.7707

PV m $284,029.1436

Total $586,402.9144

Using goal seek we find out a rate of 5% semiannually will make it.

Now we solve for thefirst interest payment:

we apply the market rate to the carrying value to know the interest expense

586,402 x 5% = 29,320.1

then we subtract the cash proceds to kwno the amortization

29,320.1 - 27,900 = 1,420.1

The carrying value is adjusted:

586,402 + 1,420.1 = 587,822.10

and the process repeat in the next payment.