Step-by-step explanation:
It is given that,
Vector 1 has a magnitude of 24 m and is pointed to the west.
Vector 2 has a magnitude of 11 and is pointed to the north.
Let v is the resultant of two vectors. The resultant of two vectors is given by :
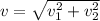
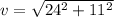
v = 26.4 m
To find direction,
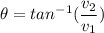
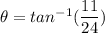
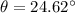
So, the magnitude and direction of the resultant vector produced by these two is 26.4 m and 24.62 degrees respectively. Hence, this is the required solution.