Answer:
15 deg
Step-by-step explanation:
Assume both snowballs are thrown with the same initial speed 27.2 m/s. The first snowball is thrown at an angle of 75◦ above the horizontal. At what angle should you throw the second snowball to make it hit the same point as the first? The acceleration of gravity is 9.8 m/s 2 . Answer in units of ◦ .
Given:
For first ball, θ1 = 75◦
initial velocity for both the balls, u = 27.2 m/s
for second ball, θ2 = ?
since distance covered by both the balls is same.
Therefore,..
R1=(u^{2} sin2\alpha _{1}) /g[/tex]
the range for the first ball
the range for the second ball
R2=(u^{2} sin2\alpha _{2}) /g[/tex]
(u^{2} sin2\alpha _{2}) /g[/tex]=(u^{2} sin2\alpha _{1}) /g[/tex]
sin2\alpha _{2})=sin2\alpha _{1})
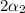 =sin^-1(sin2\alpha _{1})
=sin^-1(sin2\alpha _{1})
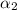 =1/2sin^-1(sin2\alpha _{1})
=1/2sin^-1(sin2\alpha _{1})
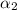 =
=
15 deg