Question

A woman at a grocery store wanted to purchase a 5 pound bag of apples but thought she would first weigh the bag on the store scale to verify the weight. The store scale read 4.5 lbs. The woman alerted the store manager of her finding. He weighed 100 bags of apples from his store and the average weight turned out to be 4.38 pounds with a SD of 0.5 pounds. After the manager contacted the packaging company, they conducted their own investigation. They weighed 100 bags of the 5 pound bags that they had just packaged at the plant and came up with an average weight of 4.95 lbs. with a SD of 0.5 pounds. Is the lower apple bag weight observed at the grocery store likely to be due to chance variation?

Answer 1

No

Explanation:

here we are interested to test the mean weight of a bag is less than 5 pound.

So null hypothesis is
`H_0:\mu =5`

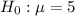
and alternative hypothesis is
`H_1:\mu <5`

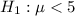
Let's do one sample z test.

The given information Sample size = n =100

sample mean
`\overline{X}=4.38`,

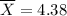standard deviation
`\sigma =0.5`

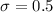
Test statistic:Z=
`\frac{\overline{X}-\mu }{(\sigma )/(√(n))}`

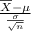
Z=
`(4.38-5)/((0.5)/(√(100)))=-12.4`

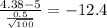
This is a left tailed test, hence the p value for the left tailed test and Z score= -12.4 is
`\approx` 0

Hence We can reject the null hypothesis to say that we have evidence that apple bag weight at the grocery store is less than 5 pounds and it is not a chance variation