Question

On the day before an election in a large city, each person in a random sample of 1,000 likely voters is asked which candidate he or she plans to vote for. Of the people in the sample, 55 percent say they will vote for candidate Taylor. A margin of error of 3 percentage points is calculated. Which of the following statements is appropriate?

a. The proportion of all likely voters who plan to vote for candidate Taylor must be the same as the proportion of voters in the sample who plan to vote for candidate Taylor (55 percent), because the data were collected from a random sample.
b. The sample proportion minus the margin of error is greater than 0.50, which provides evidence that more than half of all likely voters plan to vote for candidate Taylor.
c. It is not possible to draw any conclusion about the proportion of all likely voters who plan to vote for candidate Taylor because the 1,000 likely voters in the sample represent only a small fraction of all likely voters in a large city.
d. It is not possible to draw any conclusion about the proportion of all likely voters who plan to vote for candidate Taylor because this is not an experiment.
e. It is not possible to draw any conclusion about the proportion of all likely voters who plan to vote for candidate Taylor because this is a random sample and not a census.

Answer 1

The answer is B

Explanation:

Definition of margin of error is simply expected error from result of a survey. Which means the actual vote results are in the range of plus or minus %3.

On this survey the result is %55 percent in favor of Taylor and the margin of error is %3. That means in the real election Taylor will get votes in between %52-%58. In other word

`0.55-0.03=0.52`

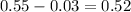
The sample proportion minus the margin of error is greater than 0.50, which provides evidence that more than half of all likely voters plan to vote for candidate Taylor.