Question

A proposed space station consists of a circular tube that will rotate about its center (like a tubular bicycle tire), Fig. 5–39. The circle formed by the tube has a diameter of 1.1 km. What must be the rotation speed (revolutions per day) if an effect nearly equal to gravity at the surface of the Earth (say, 0.90 g) is to be felt?

Answer 1

1728 rev/sec

Step-by-step explanation:

The expression for the gravitational force is given by

F_g=mg_1

g_1=0.9g (Given)

therefore,

`F_g=0.9mg`

The centripetal force balances this gravitational force to keep the space station in equilibrium.

Hence we can write

`(mv^2)/(r) =0.9mg`

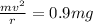
Rearrange the above equation in terms of velocity

`v=\sqrt{(0.9mgr)/(m) }`

⇒
`v=√(0.9gr)`

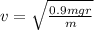
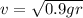
putting the values we get

`v=\sqrt{(0.9(9.81)(1100))/(2) }`

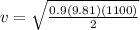
v=69.65 m/sec

the rotational speed can be calculated as or frequency of rotation

`f= (v)/(2\pi r)`

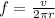
putting values we get

`f= (69.65)/(2\pi 5500)`

f= 0.02 rev/sec

meaning 0.02 rev per second

therefore no. or revolution per day

= 0.02×24×3600= 1728 rev/sec

Answer 2

1742.24106 revolutions per day

Step-by-step explanation:

v = Velocity

d = Diameter = 1.1 km

r = Radius =
`(d)/(2)=(1.1)/(2)=0.55\ km`

g = Acceleration due to gravity = 9.81 m/s²

g = 0.9 g

The centrifugal force will balance the gravitational force

`F_c=mg\\\Rightarrow (mv^2)/(r)=m0.9g\\\Rightarrow v=\sqrt{(0.9gmr)/(m)}\\\Rightarrow v=√(0.9gr)\\\Rightarrow v=√(0.9* 9.81* 0.55* 10^3)\\\Rightarrow v=69.68464\ m/s`

`(1)/(T)=(v)/(2\pi r)\\\Rightarrow (1)/(T)=(69.68464)/(2\pi 0.55* 10^3)* 24* 60* 60\\\Rightarrow (1)/(T)=1742.24106\ rev/day`

The rotation speed is 1742.24106 revolutions per day