Question

Question 9 please both a and b

Answer 1

`a^k - b^k = (a - b)(a^(k-1) + a^(k-2)b + ... + b^(k-1))`

a. Let's set a=3, b=1

`3^k - 1^k = (3 - 1)(\textrm{some integer we'll call } m)`

`3^k = 1 + 2m`

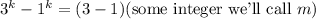
In other words
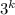`3^k` is odd, i.e.
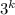`3^k` has remainder 1 when divided by 2.
`\quad\checkmark`

b. Let

`k=2n, a=3, b=1`

`a^k - b^k = (a - b)(a^(k-1) + a^(k-2)b + ... + b^(k-1))`

`3^(2n) - 1^(2n) = (3 - 1 )(3^(2n-1) + 3^(2n-2) + ... + 1)`

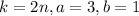
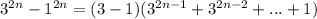
There are 2n terms in the last factor. All the terms of the form

`3^(2n-k)`

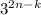
are odd. So when we add up an even number of them, we get an even number, call it 2m.

`3^(2n) - 1 = 2(2m)`

`3^(2n) - 1 = 4m`

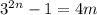
We've shown
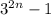`3^(2n)-1` is divisible by four.
`\quad \checkmark`

Merry Christmas!