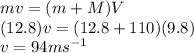Answer:
94 ms⁻¹
Step-by-step explanation:
 = Speed of the bullet-block combination after collision
= Speed of the bullet-block combination after collision
 = distance traveled by the combination before coming to stop = 6.5 m
= distance traveled by the combination before coming to stop = 6.5 m
 = Coefficient of kinetic friction = 0.750
= Coefficient of kinetic friction = 0.750
acceleration due to friction on a flat surface can be given as
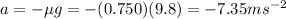
 = Final speed of the combination = 0 m/s
= Final speed of the combination = 0 m/s
Based on the above equation , we can use the kinematics equation as
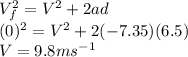
 = mass of the wooden block = 110 g
= mass of the wooden block = 110 g
 = mass of the bullet = 12.8 g
= mass of the bullet = 12.8 g
 = Speed of the bullet before collision
= Speed of the bullet before collision
Using conservation of momentum for inelastic collision , we have