Question

Legalization of marijuana, Part I. The 2010 General Social Survey asked 1,259 US res- idents: \Do you think the use of marijuana should be made legal, or not?" 48% of the respondents said it should be made legal.44 (a) Is 48% a sample statistic or a population parameter? Explain. (b) Construct a 95% condence interval for the proportion of US residents who think marijuana should be made legal, and interpret it in the context of the data. (c) A critic points out that this 95% condence interval is only accurate if the statistic follows a normal distribution, or if the normal model is a good approximation. Is this true for these data? Explain. (d) A news piece on this survey's ndings states, \Majority of Americans think marijuana should be legalized." Based on your condence interval, is this news piece's statement justied?

Answer 1

0.4524, 0.5076), Not necessary, not supported

Explanation:

a)Since 48% is the sample proportion for a sample of 1259 US residents, it is a characteristic of a sample hence it is a statistic

b) For 95% confidence interval first we calculate std error

STd error =
`√(pq/n) \\\\=0.0141`

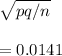
Margin of error for 95% = ±1.96*0.0141=0.0276

Confidence interval 95% = (0.48±0.0276)

=(0.4524, 0.5076)

We are 95% confidence that for samples of large size randomly drawn, the sample proportion falls within this range inside the interval

c) No, it need not be normal. The conditions are only

samples should be randomly drawn, and sample size should be sufficiently large to represent the population

d) We find that the confidence interval contains 0.50 and also mid value below 0.50

Hence the confidence interval does not support the news piece statement because it is evident only 50% support and not more than 50%