Question

Notice that all the initial spring potential energy was transformed into gravitational potential energy. If you compressed the spring to a distance of 0.200 m , how far up the slope will an identical ice cube travel before reversing directions? Note that the spring is compressed twice as much as in the original problem.

Answer 1

The question doesn't provide enough data to be solved, but I'm assuming some magnitudes to help you to solve your own problem

Answer:

The maximum height is 0.10 meters

Step-by-step explanation:

Energy Transformation

It's referred to as the change of one energy from one form to another or others. If we compress a spring and then release it with an object being launched on top of it, all the spring (elastic) potential energy is transformed into kinetic and gravitational energies. When the object stops in the air, all the initial energy is now gravitational potential energy.

If a spring of constant K is compressed a distance x, its potential energy is

`\displaystyle P_E=(Kx^2)/(2)`

When the launched object (mass m) reaches its max height h, all that energy is now gravitational, which is computed as

`U=mgh`

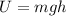
We have then,

`U=P_E`

`\displaystyle mgh=(Kx^2)/(2)`

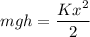
Solving for h

`\displaystyle h=(Kx^2)/(2mg)`

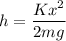
We have little data to work on the problem, so we'll assume some values to answer the question and help to solve the problem at hand

Let's say: x=0.2 m (given), K=100 N/m, m=2 kg

Computing the maximum height

`\displaystyle h=((100)0.2^2)/(2(2)(9.8))`

`\displaystyle h=(4)/(39.2)=0,10\ m`

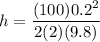
The maximum height is 0.10 meters