Question

Mark creates a graphic organizer to review his notes about electrical force. Which labels belong in the regions marked X and Y?

a. X: Decreasing to half will quadruple force Y: Doubling will double force
b. X: Doubling will cut force in half Y: Decreasing to half will cut force in half
c. X: Doubling will double force Y: Decreasing to half will quadruple force
d. X: Decreasing to half will double force Y: Doubling will cut force in half

Answer 1

X: Decreasing to half will quadruple force

Y: Doubling will double force

Answer 2

The correct answer is A

Step-by-step explanation:

The question requires as well the attached image, so please see that below.

Coulomb's Law.

The electrical force can be understood by remembering Coulomb's Law, that describes the electrostatic force between two charged particles. If the particles have charges
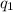`q_1` and
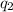`q_2`, are separated by a distance r and are at rest relative to each other, then its electrostatic force magnitude on particle 1 due particle 2 is given by:

`|F|=k \cfrac{q_1 q_2}{r^2}`

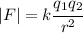
Thus if we decrease the distance by half we have

`r_1 =\cfrac r2`

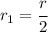
So we get

`|F|=k \cfrac{q_1 q_2}{r_1^2}`

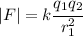
Replacing we get

`|F|=k \cfrac{q_1 q_2}{(r/2)^2}\\|F|=k \cfrac{q_1 q_2}{r^2/4}`

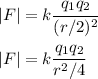
We can then multiply both numerator and denominator by 4 to get

`|F|=k \cfrac{4q_1 q_2}{r^2}`

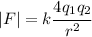
So we have

`|F|=4 \left(k \cfrac{q_1 q_2}{r^2}\right)`

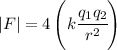
Thus if we decrease the distance by half we get four times the force.

Then we can replace the second condition

`q_(2new) =2q_2`

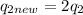
So we get

`|F|=k \cfrac{q_1 q_(2new)}{r_1^2}`

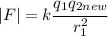
which give us

`|F|=k \cfrac{q_1 2q_2}{r_1^2}\\|F|=2\left(k \cfrac{q_1 q_2}{r_1^2}\right)`

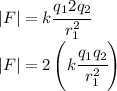
Thus doubling one of the charges doubles the force.

So the answer is A.