Question

A student believes that less than 50% of students at his college receive financial aid. A random sample of 120 students was taken. Sixty-five percent of the students in the sample receive financial aid. Test the hypothesis at the 2% level of significance. What are the p-value and conclusion? a. .999; Do not reject H0 b. .02; Reject H0

Answer 1

P-value is greater than the significance level, we fail to reject null hypothesis.

Step-by-step explanation:

Here,

Sample size = n = 120

Sample proportion = p = 0.6500

Population Proportion =
`P_(0)` = 0.5

Level of significance = α = 0.02

Step 1:

`H_(0)`: p = 0.5

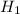`H_(1)`: p < 0.5 (Left tailed test)

Step 2:

The critical vale is = 2.0537

Step 3:

The test statistic is,

z =
`\frac{p - p_(0) }{\sqrt{(p_(0) (1-p_(0)) )/(n) } }`

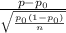
Step 5:

Conclusion using critical value: Since the test statistic value is greater than the critical value, we fail to reject null hypothesis.

Step 6:

Conclusion using P-value: Since the P-value is greater than the significance level, we fail to reject the null hypothesis.