Answer:
a)

b)
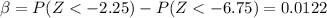
c)
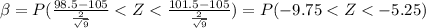

And we can see that this value is lower compared to part b. And the reason why is because when the true mean is 105 we are far from the interval of (98.85; 101.5).
Explanation:
Part a) If the acceptance region is defined as 98.5 ≤
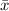 ≤ 101.5, find the type I error probability α
≤ 101.5, find the type I error probability α
For this case we need to remember the definition of the significance level
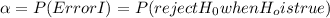
The system of hypothesis on this case are:
Null hypothesis:

Alternatibe hypothesis:
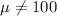
The population deviation is given
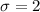 and the sample size is n=9
and the sample size is n=9
The acceptance region on this case is given by:
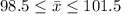
If we use the definition of probability of error I we got:
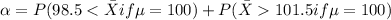
Using the definition of z score we got:
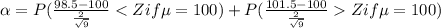

Part b: Find β for the case in which the true mean heat evolved is 103
From the definition of Type of Error II we have this:
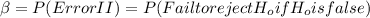
We are assuming that the true mean is 103 so we have this:

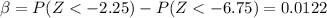
Part c: c. Find β for the case where the true mean heat evolved is 105. This value of β is smaller than the one found in part (b). Why?
From the definition of Type of Error II we have this:
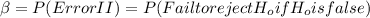
We are assuming that the true mean is 105 so we have this:
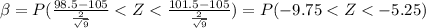

And we can see that this value is lower compared to part b. And the reason why is because when the true mean is 105 we are far from the interval of (98.85; 101.5).