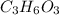Question

1. Lactic acid, which contains C, H, and O, has long been thought to be responsible for muscle soreness following strenuous exercise. When 5.000 g of lactic acid was subjected to combustion analysis, it produced 7.329 g of CO 2 and 3.000 g of H 2 O.

Answer 1

The empirical formula is =
`CH_2O`

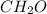
The formula of lactic acid =
`C_3H_(6)O_3`

Step-by-step explanation:

Corrected from source, empirical formula and molecular formula of the lactic acid is to be determined.

Mass of water obtained = 3.000 g

Molar mass of water = 18 g/mol

Moles of
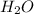`H_2O` = 3.000 g /18 g/mol = 0.1667 moles

2 moles of hydrogen atoms are present in 1 mole of water. So,

Moles of H = 2 x 0.1667 = 0.3333 moles

Molar mass of H atom = 1.008 g/mol

Mass of H in molecule = 0.3333 x 1.008 = 0.3359 g

Mass of carbon dioxide obtained = 7.329 g

Molar mass of carbon dioxide = 44.01 g/mol

Moles of
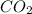`CO_2` = 7.329 g /44.01 g/mol = 0.1665 moles

1 mole of carbon atoms are present in 1 mole of carbon dioxide. So,

Moles of C = 0.1665 moles

Molar mass of C atom = 12.0107 g/mol

Mass of C in molecule = 0.1665 x 12.0107 = 2.0001 g

Given that the Lactic acid only contains hydrogen, oxygen and carbon. So,

Mass of O in the sample = Total mass - Mass of C - Mass of H

Mass of the sample = 5.000 g

Mass of O in sample = 5.000 - 2.0001 - 0.3359 = 2.6641 g

Molar mass of O = 15.999 g/mol

Moles of O = 2.6641 / 15.999 = 0.1665 moles

Taking the simplest ratio for H, O and C as:

0.3333 : 0.1665 : 0.1665

= 2 : 1 : 1

The empirical formula is =
`CH_2O`

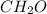
Molecular formulas is the actual number of atoms of each element in the compound while empirical formulas is the simplest or reduced ratio of the elements in the compound.

Thus,

Molecular mass = n × Empirical mass

Where, n is any positive number from 1, 2, 3...

Mass from the Empirical formula = 1×12 + 2×1 + 16= 30 g/mol

Molar mass = 90.08 g/mol

So,

Molecular mass = n × Empirical mass

90.08 = n × 30

⇒ n = 3

The formula of lactic acid =
`C_3H_(6)O_3`