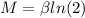Question

The median of a probability distribution can be defined as the number m such that Upper P (Upper X less than or equals m )equals Upper P (Upper X greater than or equals m ). Find an expression for the median m of the exponential distribution.

Answer 1

tex]M=\beta ln(2)[/tex]

Explanation:

Previous concepts

The exponential distribution is "the probability distribution of the time between events in a Poisson process (a process in which events occur continuously and independently at a constant average rate).

Solution to the problem

For this case we can use the following Theorem:

"If X is a continuos random variable of the exponential distribution with parameter
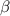`\beta` for some
`\beta \in R >0`"

Then the median of X is
`\beta ln (2)`

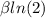
Proof

Let M the median for the random variable X.

From the definition for the exponential distribution we know the denisty function of X is given by:

`f_X (x) = (1)/(\beta) e^{-(x)/(\beta)}`

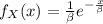
Since we need the median we can put this equation:

`P(X<M) = (1)/(\beta) \int_0^(M) e^{- (x)/(\beta)} dx = 1/2`

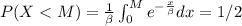
If we evaluate the integral we got this:

`(1)/(\beta) \int_0^M e^{- (x)/(\beta)}dx =(1)/(\beta) [-\beta e^{-(x)/(\beta)}] \Big|_0^M`

And that's equal to:

`1/2 = 1 -e^{- (M)/(\beta)}`

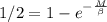
And if we solve for M we got:

`1-e^{- (M)/(\beta)} = (1)/(2)`

`e^{- (M)/(\beta)}=(1)/(2)`

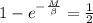
If we apply natural log on both sides we got:

`-(M)/(\beta)=ln(1/2)`

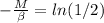
And then
`M=\beta ln(2)`