Question

1) Ten samples of a process measuring the number of returns per 100 receipts were taken for a local retail store.

The number of returns were 10, 9, 11, 7, 3, 12, 8, 4, 6, and 11.

Find the standard deviation of the sampling distribution for the p-bar chart.

A) There is not enough information to answer the question.

B) .081

C) 8.1

D) .0273

E) .0863

Answer 1

E) .0863

Explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The population proportion have the following distribution

`p \sim N(p,\sqrt{(p(1-p))/(n)})`

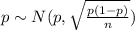
Solution to the problem

For this case we can find the sample proportion for each observation with the following formula:

`\hat p = (X)/(n)`

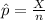
Where X represent the number of returns and n =100 for each case since the standard value used. Using the last formula we got:

`p_1 = (10)/(100)=0.1`

`p_2 = (9)/(100)=0.09`

`p_3 = (11)/(100)=0.11`

`p_4 = (7)/(100)=0.07`

`p_5 = (3)/(100)=0.03`

`p_6 = (12)/(100)=0.12`

`p_7 = (8)/(100)=0.08`

`p_8 = (4)/(100)=0.04`

`p_9 = (6)/(100)=0.06`

`p_(10) = (11)/(100)=0.11`

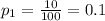
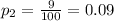
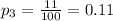
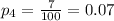
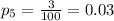
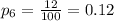
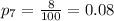
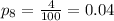
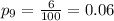
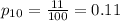
And now witht those values we can find the sample mean of proportions with the following formula:

`hat p = (\sum_(i=1)^n p_i)/(n)= (0.1+0.09+0.11+0.07+0.03+0.12+0.08+0.04+0.06+0.11)/(10)=0.081`

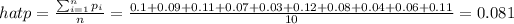
And we can find the standard error with the following formula:

`SE= \sqrt{(\hat p (1-\hat p))/(n)}=\sqrt{(0.081(1-0.081))/(10)}=0.0863`

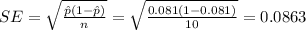
So then the best option on this case is given by:

E) .0863