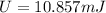Question

A wire is wrapped 200 times around a hollow cylinder of cross-sectional area 12 cm2 and length 10 cm. Assuming the turns are spread out evenly over the length of the cylinder, how much energy is stored in this coil when the wire carries a current of 6 A

Answer 1

The answer is 10.857mJ

Step-by-step explanation:

The energy stored in this solenoid is given by the below mentioned equation,

`U = L*I^(2)/2`

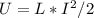
where L the inductance of this solenoid is given by the below mentioned equation,

`L = u_(0) *N^(2)*A/L`

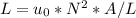
Plugging this into the energy equation you obtain the equation for the total energy stored in the magnetic field of the solenoid, given by,

`U = u_(0) *N^(2)*A*I^(2)/(2*L)`

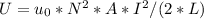
where
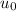`u_(0)` is the permeability of free space which equals to
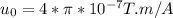`u_(0) = 4*\pi *10^(-7) T.m/A`. Plugging all the quantities into the above equation from the data in the question after converting to standard units. of meters instead of centimeters, we get for the energy stored in the coil,

`U = 10.857mJ`