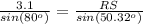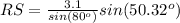Question

asked Jan 15, 2020 207k views

2 Answers

Silo · Answer 1 · 2020-01-20T04:43:38+0000

Answer:

$RS=2.4\ units$

Explanation:

The complete question is

What is the length of line segment RS? Use the law of sines to find the answer. Round to the nearest tenth.

see the attached figure to better understand the problem

step 1

Find the measure of angle S

Applying the law of sines

(QS)/(sin(R))=(QR)/(sin(S))

substitute the given values

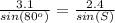
(3.1)/(sin(80^o))=(2.4)/(sin(S))

Solve for sin(S)

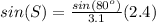
sin(S)=(sin(80^o))/(3.1)(2.4)

$S=sin^(-1)[sin(80^o)}{3.1}(2.4)]$

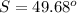
S=49.68^o

step 2

Find the measure of angle Q

Remember that the sum of the interior angles in any triangle mut b equal to 180 degrees

so

$m\angle Q+m\angle R+m\angle S=180^o$

substitute the given values

$m\angle Q+80^o+49.68^o=180^o$

$m\angle Q+129.68^o=180^o$

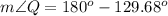
$m\angle Q=180^o-129.68^o$

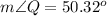
$m\angle Q=50.32^o$

step 3

Find the length of segment RS

Applying the law of sines

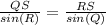
(QS)/(sin(R))=(RS)/(sin(Q))

substitute the given values

(3.1)/(sin(80^o))=(RS)/(sin(50.32^o))

$RS=(3.1)/(sin(80^o)){sin(50.32^o)}$

$RS=2.4\ units$

Please log in or register to add a comment.