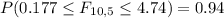Answer:
a)
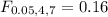
b)
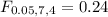
c)
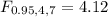
d)
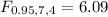
e)
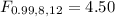
f)
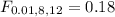
g)
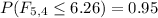
h)
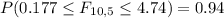
Explanation:
(a) F0.05, 4, 7 (Round your answer to two decimal places.)
For this case we need a valueof the F distribution with 4 degrees of freedom for the numerator and 7 for the denominator that accumulates 0.05 of the area on the left tail. We can use the following excel code: "=F.INV(0.05,4,7)". And we got:
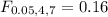
(b) F0.05, 7, 4 (Round your answer to two decimal places.)
For this case we need a valueof the F distribution with 7 degrees of freedom for the numerator and 4 for the denominator that accumulates 0.05 of the area on the left tail. We can use the following excel code: "=F.INV(0.05,7,4)". And we got:
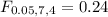
(c) F0.95, 4, 7 (Round your answer to three decimal places.)
For this case we need a valueof the F distribution with 4 degrees of freedom for the numerator and 7 for the denominator that accumulates 0.95 of the area on the left tail. We can use the following excel code: "=F.INV(0.95,4,7)". And we got:
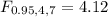
(d) F0.95, 7, 4 (Round your answer to three decimal places.)
For this case we need a valueof the F distribution with 7 degrees of freedom for the numerator and 4 for the denominator that accumulates 0.95 of the area on the left tail. We can use the following excel code: "=F.INV(0.95,7,4)". And we got:
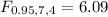
(e) the 99th percentile of the F distribution with v1 = 8, v2 = 12 (Round your answer to two decimal places.)
So for this case we need a value on the F distribution with 8 degrees of freedom for the numerator and 12 for the denominator that accumulates 0.99 of the area on the left tail. And we can use the following excel code: "=F.INV(0.99,8,12)". And we got:
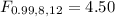
(f) the 1st percentile of the F distribution with v1 = 8, v2 = 12 (Round your answer to three decimal places.)
So for this case we need a value on the F distribution with 8 degrees of freedom for the numerator and 12 for the denominator that accumulates 0.01 of the area on the left tail. And we can use the following excel code: "=F.INV(0.01,8,12)". And we got:
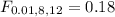
(g) P(F ≤ 6.26) for v1 = 5, v2 = 4 (Round your answer to two decimal places.)
For this case we want to find the probability that the F distribution with 5 degrees on the numerator and 4 on the denominator would be less or equal than 6.26. We can use the following excel code: "=F.DIST(6.26,5,4,TRUE)". And we got
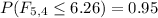
(h) P(0.177 ≤ F ≤ 4.74) for v1 = 10, v2 = 5 (Round your answer to two decimal places.)
For this case we want to find the probability that the F distribution with 10 degrees on the numerator and 5 on the denominator would be between 0.177 and 4.74. We can use the following excel code: "=F.DIST(4.74,10,5,TRUE)-F.DIST(0.177,10,5,TRUE)". And we got