To solve this problem it is necessary to apply the concepts related to the capacitance in the disks, the difference of the potential and the load in the disc.
The capacitance can be expressed in terms of the Area, the permeability constant and the diameter:
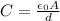
Where,
 = Permeability constant
= Permeability constant
A = Cross-sectional Area
d = Diameter
Potential difference between the two disks,
V = Ed
Where,
E = Electric field
d = diameter
Q = Charge on the disk equal to

Through the value found and the expression given for capacitance and potential, we can define the electric charge as
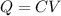
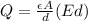
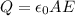
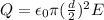
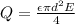
Re-arranging the equation to find the diameter of the disks, the equation will be:
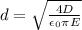
Replacing,

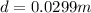
Therefore the diameter of the disks is 0.03m