Answer:
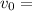 1.71
1.71
Step-by-step explanation:
the parabolic movment is described by the following equation:
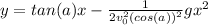
where y is the height of the ball, a is the angle of launch,
 the initial velocity, g the gravity and x is the horizontal distance of the ball.
the initial velocity, g the gravity and x is the horizontal distance of the ball.
So, if we want that the ball reach the hood, we will replace values on the equation as:
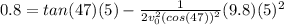
Finally, solving for
 , we get:
, we get:

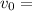 1.71
1.71