Question

The gestation time of humans has an approximate Normal distribution with a mean of 250 days and a standard deviation of 6.0 days. A simple random sample of newborns is taken. How large of a sample is needed so that the sampling distribution of has a standard deviation of 1 day

Answer 1

36

Explanation:

The variance of one human is σ² = 36 days. Each gestation time for each human of the sample is independant of the other.

Both variance and mean of the sum of identically distributed indipendant random variables is equivalent to the product of the variance/mean of one element of the sample by the sample length.

Therefore, if we take the sum n of random variables with variance 36, then the variance of the sum will be 36*n. The sampling distribution is obtained from the sum by dividing by n. If we divide by a number, then the variance will be divided by its square. So the variance of the sampling distribution is 36*n/n² = 36/n, and the standard deviation is 6/√n days.

If we want the sampling distribution to have standard deviation equal to 1 day, then we need n such that

`(6)/(√(n)) = 1 \, \rightarrow √(n) = 6 \, \rightarrow n = 36`

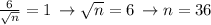
This shows that the sample length should be 36.