Question

An old millstone, used for grinding grain in a gristmill, is a solid cylindrical wheel that can rotate about its central axle with negligible friction. The radius of the wheel is 0.330 m. A constant tangential force of 200 N applied to its edge causes the wheel to have an angular acceleration of 0.924 rad/s (a) What is the moment of inertia of the wheel (in kg m2)? kg m2 (b) What is the mass (in kg) of the wheel? kg (c) The wheel starts from rest and the tangential force remains constant overa time period speed (in rad/s) of the wheel at the end of this time period? of 5.50 s. What is the angular rad/s

Answer 1

71.42857 kgm²

1311.81946 kg

5.082 rad/s

Step-by-step explanation:

F = Force = 200 N

R = Radius = 0.33 m

`\alpha` = Angular acceleration is 0.924 rad/s²

Moment of inertia is given by

`I=(FR)/(\alpha)\\\Rightarrow I=(200* 0.33)/(0.924)\\\Rightarrow I=71.42857\ kgm^2`

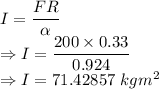
The moment of inertia of the wheel is 71.42857 kgm²

Moment of inertia of a solid cylindrical wheel is given by

`I=(1)/(2)mR^2\\\Rightarrow m=(2I)/(R^2)\\\Rightarrow m=(2* 71.42857)/(0.33^2)\\\Rightarrow m=1311.81946\ kg`

The mass of the wheel is 1311.81946 kg

Rotational impulse is given by

`I_r=\tau t\\\Rightarrow I_r=FRt`

Also

`I_r=I(\omega_f-\omega_i)\\\Rightarrow I_r=I(\omega_f-0)\\\Rightarrow I_r=I\omega_f\\\Rightarrow \omega_f=(I_r)/(I)`

`\omega_f=(FRt)/(I)\\\Rightarrow \omega_f=(200* 0.33* 5.5)/(71.42857)\\\Rightarrow \omega_f=5.082\ rad/s`

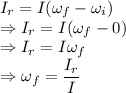
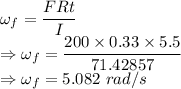
The angular speed is 5.082 rad/s