Question

Among uses of automated teller machines​ (ATMs), 92​% use ATMs to withdraw cash and 29​% use them to check their account balance. Suppose that 95​% use ATMs to either withdraw cash or check their account balance​ (or both). Given a woman who uses an ATM to check her account​ balance, what the probability that she also uses an ATM to get​ cash? The probability is nothing.

Answer 1

`P(A|B) =(P(A and B))/(P(B))=(0.26)/(0.29)=0.897`

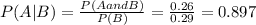
Explanation:

Data given

Lets define the following events

A: An user use ATMs to withdraw cash

B: An user use ATMs to check their account balance

92​% use ATMs to withdraw cash

29​% use them to check their account balance

95​% use ATMs to either withdraw cash or check their account balance​ (or both)

For this case we have some probabilities given:

P(A) =0.92, P(B) =0.29 and P(A U B)=0.95

Solution to the problem

On this case we want to find this probability:

P(A|B) the conditional probability.

By defintion of conditional probability we know that:

`P(A|B) =(P(A and B))/(P(B))`

In order to find P(A and B) we can use the total probability rule given by:

P(A U B) =P(A)+ P(B) -P(A and B)

And solving for P(A and B) we got:

P(A and B) =P(A) +P(B) -P(AUB) =0.92+0.29-0.95=0.26

And now we can replace in the conditional formula like this:

`P(A|B) =(P(A and B))/(P(B))=(0.26)/(0.29)=0.897`

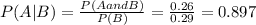
And then, given a woman who uses an ATM to check her account​ balance, what the probability that she also uses an ATM to get​ cash the probability is 0.897