Answer:
9.9 s
Step-by-step explanation:
mass (m) = 1000 kg
initial speed (u) = 90 km/h
final speed (v) = 45 km/h
relationship between the speed (v) of the boat and the frictional force (fk) ⇒ fk = 70v
- the acceleration of the system will be given by (a) =
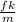
- acceleration is also the first differential of velocity with respect to time,
a =
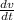
- therefore acceleration (a) =
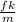 =
=
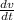
- recall that fk = 70v
(a) =
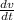 =
=
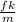 =
=
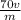
(a) =
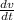 =
=
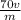
- integrating both side of the equatin we have
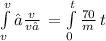
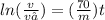
t =
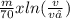
- the time required for the boat to slow down = t =
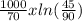 = - 9.9 s = 9.9 s
= - 9.9 s = 9.9 s