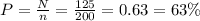Question

2. An exam readiness awareness taskforce at a Fremont National university sampled 200 students after the midterm to ask them whether they went partying the week-end before the midterm or spent the week-end studying, and whether they did well or poorly on the midterm. The following result was obtained:Did Well on the Midterm Did Poorly on the Midterm Studied for the Midterm 75 25 Went Partying 40 60 1. Referring to the table above, what is the probability that a randomly selected student did poorly on the midterm or went partying the weekend before the midterm? a) (40/200) or 20% b) (75+40+25)/200 or 70% c) (40+60+25)/200 or 63% d) (75+40+60/200 or 88% e) None of the above

Answer 1

c) (40+60+25)/200 or 63%

Explanation:

n= 200 students

Did Well on the Midterm and Studied for the Midterm = 75

Did Well on the Midterm and Went Partying = 40

Did Poorly on the Midterm and Studied for the Midterm = 25

Did Poorly on the Midterm and Went Partying = 60

The number of students that did poorly on the midterm or went partying the weekend before the midterm is given by the sum of all students who did poorly to all students who went partying minus the number of students who did Poorly on the Midterm and Went Partying:

`N=(25+60)+(40+60) - 60\\N= 125`

The probability that a randomly selected student did poorly on the midterm or went partying the weekend before the midterm is given by:

`P = (N)/(n)=(125)/(200) = 0.63 = 63\%`