Question

Consider the following reaction. SO2Cl2 → SO2 + Cl2. After collecting experimental data you found that plotting ln[SO2Cl2] vs. time (s) fit a straight line with the following formula. y = -0.000290t-2.30 Using this information, what is the concentration of SO2Cl2 at 600 s?

Answer 1

`[SO_2Cl_2]_(600)= 0.0842 M`

Step-by-step explanation:

Some theoretical knowledge is required here. We should understand that whenever we plot the natural logarithm, ln, of a concentration vs. time and obtain a straight line, this indicates a first-order reaction. That said, since this is the case here, we have a first-order reaction with respect to
`SO_2Cl_2`.

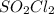The linear equation has the following terms:

`y = -0.000290t - 2.30`

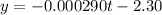
It is a linear form of the integrated first-order law equation:

`ln[SO_2Cl_2]_t = -kt + ln[SO_2Cl_2]_o`

Therefore, the rate constant, k, is:

`k = 0.000290 s^(-1)`

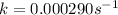
The natural logarithm of initial molarity is:

`ln[SO_2Cl_2]_o = -2.30`

Using the equation, we may substitute for t = 600 s and obtain the natural logarithm of the concentration at that time:

`ln[SO_2Cl_2]_(600) = -0.000290 s^(-1)\cdot 600 s - 2.30 = -2.474`

Take the antilog of both sides to find the actual molarity:

`[SO_2Cl_2]_(600)=e^(-2.474) = 0.0842 M`