Question is Incomplete,Complete Question is below.
D is a point on the side BC of a triangle ABC such that angle ADC = angle BAC Show that CA square=CB .CD
Answer:
The Proof is given below.
Explanation:
Given:
In ΔABC,
∠ADC = ∠BAC
To Show:
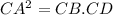
Proof:
In ΔBAC and ΔADC
∠ADC = ∠BAC ............................Given
∠C = ∠C .....................................Reflexive Property
∴ ΔBAC ~ ΔADC .................... A-A similarity test
If two triangles are similar then their sides are in proportion.
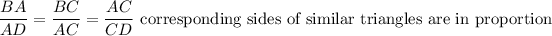
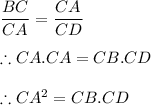 ..........Proved
..........Proved