Answer:
The mass of the block is 0.025 kg
Step-by-step explanation:
Mass-Spring Harmonic Motion
When a mass m is attached to a spring of constant k, they produce a simple harmonic motion which angular frequency is
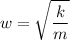
We also know
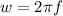
which means

Squaring
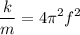
Solving for m

We have
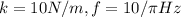
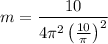
Operating
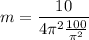
Simplifying and computing

The mass of the block is 0.025 kg