Answer:
V' = -0.11552 *V\\= -0.11552(1.8)\\ \\=-0.20794 million per year
Explanation:
Given that oil is pumped continuously from a well at a rate proportional to the amount of oil left in the well. Initially there were 3 million barrels of oil in the well; six years later 1,500,000 barrels remain.
i.e. if V stands for volume of oil, then
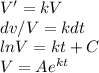
To find A and k
V(0) = A = 3 million
Hence V =
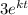
V(6) = 1.5
i.e.
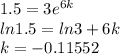
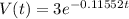
a) Using the above value of k , we have
 million per year.
million per year.