Question

Suppose at a large university, 60% of the students have a Visa card and 40% of the students have a MasterCard. Also, 30% of the students neither have 1 a Visa card, nor have a MasterCard. Randomly select a student from the university. Given that this student has a Visa card, what is the probability that this student also has a MasterCard1. Calculate the probability that this student does not have a MasterCard. 2. Calculate the probability that this student has either a Visa card or a MasterCard. 3. Calculate the probability that this student has neither a Visa card nor a MasterCard. 4. Are the events A and B disjoint? Are the events A and B independent?

Answer 1

0.6,0.7,0.3 neither disjoint nor independent.

Explanation:

Given that at a large university, 60% of the students have a Visa card and 40% of the students have a MasterCard.

A= visa card

B = Master card

P(A) = 0.60 and P(B) = 0.40

P(AUB)' = 0.30

i.e. P(AUB) = 0.70

Or P(A)+P(B)-P(AB) =0.70

P(AB)= 0.30

Randomly select a student from the university.

1) the probability that this student does not have a MasterCard.

`= P(B') = 1-0.4 =0.6`

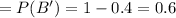
2. the probability that this student has either a Visa card or a MasterCard.

=
`P(AUB) = 0.70`

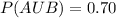
3. Calculate the probability that this student has neither a Visa card nor a MasterCard.

=
`P(AUB)' = 0.30`

4. Are the events A and B disjoint? Are the events A and B independent?

A and B have common prob 0.30 hence not disjoint.

P(AB) ≠P(A)P(B)

Hence not independent