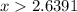Question

Attachment below
algebra helppppp

Answer 1

Answer: second option.

Explanation:

In order to solve this exercise, it is necessary to remember the following properties of logarithms:

`1)\ ln(p)^m=m*ln(p)\\\\2)\ ln(e)=1`

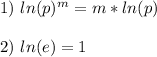
In this case you have the following inequality:

`e^x>14`

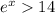
So you need to solve for the variable "x".

The steps to do it are below:

1. You need to apply
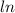`ln` to both sides of the inequality:

`ln(e)^x>ln(14)`

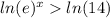
2. Now you must apply the properties shown before:

`(x)ln(e)>ln(14)\\\\(x)(1)>2.63906\\\\x>2.63906`

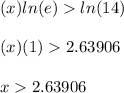
3. Then, rounding to the nearest ten-thousandth, you get:

`x>2.6391`