Question

A 2-kg object is initially at the bottom of a long 50° inclined plane, and is beginning to slide up this inclined plane. The initial velocity of the object os 3.0 m/s. The coefficient of kinetic friction between the object and the surface of the inclined plane is µk = 0.3, while the coefficient of static friction is µs = 0.4. Will the object ever slide back down to the initial position? If yes, what will be its speed once it slides back down to the bottom? If no, how high up the incline will it manage to climb?

Answer 1

Step-by-step explanation:

Given

mass of object
`m=2 kg`

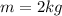
inclination
`\theta =50^(\circ)`

`\mu _k=0.3`

`\mu _s=0.4`

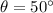
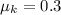
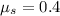
initial velocity
`u=3 m/s`

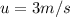
acceleration of block during upward motion

`a=g\sin \theta -\mu _kg\cos \theta`

`a=g(\sin 50-0.3\cos 50)`

`a=5.617 m/s^2`

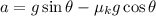
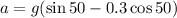
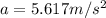
using relation

`v^2-u^2=2a\cdot s`

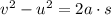
where
`s=distance\ moved`

`v=final\ velocity`

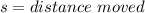
v=0 because block stopped after moving distance s

`0-(3)^2=2\cdot (-5.617)\cdot s`

`s=(4.5)/(5.617)`

`s=0.801`

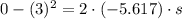
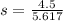
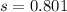
If block stopped after s m then force acting on block is

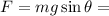`F=mg\sin \theta =`friction force
`f_r=\mu mg\cos \theta`

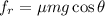
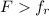`F>f_r` therefore block will slide back down to the bottom