Question

Assume that your parents wanted to have $ 130,000 saved for college by your 18th birthday and they started saving on your first birthday. They saved the same amount each year on your birthday and earned 5.5 % per year on their investments.

(a) How much would they have to save each year to reach their​ goal?
(b) If they think you will take five years instead of four to graduate and decide to have $ 170,000 saved just in​ case, how much would they have to save each year to reach their new​ goal?

Answer 1

A) $4,409.8

B) $5,766.6

Step-by-step explanation:

A)

To answer the first question, we must use the future value of an ordinary annuity formula:

`FV = A ((1+i)^(n) -1)/i`

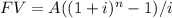
Where:

FV = Future value of the investment

A = Value of annuity

i = Interest rate

n = number of compounded periods

Now we simply plug the amounts into the formula:

130,000 = A ((1 + 0.055)^18-1) / 0.055

130,000 = A (29.48)

130,000 / 29.48 = A

$4,409.8 = A

Therefore, the parents would have to add $4,409.8 dollars each year to the college fund.

B)

To answer the second question, we use the same formula, only the values change:

170,000 = A ((1 + 0.055)^18-1) / 0.055

170,000 = A (29.48)

170,000 / 29.48 = A

$5,766.6 = A

Therefore, to have $170,000 saved by the 18th year, the parents would have to add $5,766.6 per year to the fund.